Simpler ≠ faster : you still have to know what happens “under the hood”.
If you read the post about en masse operations, you might remember that I pointed out that you should know what is happening behind the scenes. Here is a particular case where what looks like simpler code actually takes longer to execute. If you don’t take the time to think about what is actually going on, then you might be fooled.
Consider a pair of signals, each around 12000 samples. Regulations state that I am allowed to drop (delete) certain samples from those signals before performing statistical operations on them. The number of points to be dropped might be 2-10%, or up to 1200 of the points. I have the indexes to be dropped in a third array. For graphing purposes, I need to keep the dropped points in separate arrays.
Now every programmer worth his salt has fallen into the trap of deleting elements 3, 5, and 8 from an array: If you try the straightforward way, you find out that after you delete element 3, that element 5 is not in the same place it was before! So you either have to delete element 8 BEFORE you delete element 5 and then 3, or you have to delete element (3-0), then element (5-1), and then element (8-2).
Having fallen into that pothole my share of times many years ago, I avoided it this time by doing the reversing trick: My list of points to drop was known to be in ascending order, so I reversed it, and then did the deletions. Because I needed the deleted points in proper order, I had to reverse those after the deletion. Here’s the code:
That worked fine for some time, but while revisiting this code, it occurred to me that it might be faster to manipulate the index while deleting, and avoid the reversals and speed things up. Here’s the code:
That’s certainly simpler, right? As one should always do, I applied a Timing Measurement to it. And I was surprised. I created two arrays of 12000 numbers and an array of 1200 random (0..11999) indexes. It was consistently 5-6% MORE TIME this simpler way.
But if you stop and think about what’s going on, the reason is clear. Suppose your signal array contains [0, 1, 2, 3, 4, 5] and you want to delete elements [1, 3, 4 ]
Using method A you reverse the list to get [4, 3, 1 ].
You delete element 4. {that moves element 5 down – 1 move}
You delete element 3. {that moves element 5 down – 1 more move}
You delete element 1. {that moves elements 2, 5 down – 2 more moves}
That’s 4 moves that were made in the shuffling process.
Now consider the “simpler” method:
You delete element [1-0]. {that moves elements 2,3,4,5 down = 4 moves }
You delete element [3-1]. {that moves elements 4,5 down = 2 moves}
You delete element [4-2]. {that moves element 5 down = 1 move }
That’s a total of SEVEN moves that were made.
So even though we eliminated three REVERSAL operations, we actually take LONGER because we are doing more work. The increased amount of data-shuffling was enough to overcome the benefit of removing the reversals.
This was done using a random list of indexes to drop; I’d bet that there are possible scenarios where this wouldn’t hold true (for example if the points to drop were few, and confined to the end of the signal), but given that neither of those will be true in my case, I’m sticking with the original plan – on average it will be faster.
But don’t assume that fewer operations on the diagram means less work !

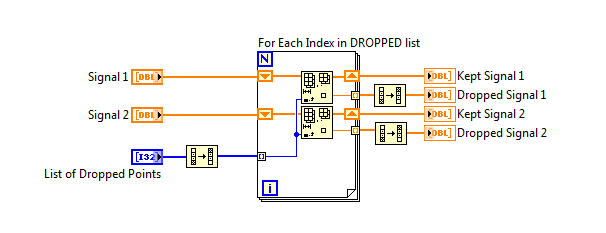
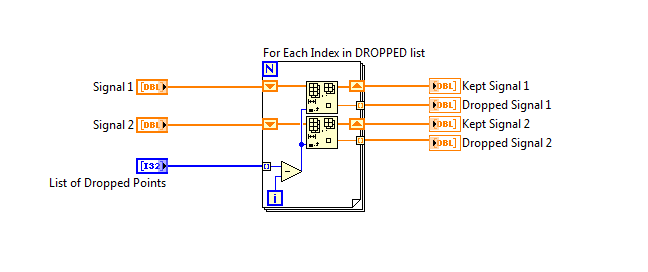

Your “simpler” method is also wrong. You are subtracting from the index, rather than subtracting I from N and indexing the indexes array.
No, Paul, it’s correct. This is the “pothole” I was referring to – look at it again.
The array is [ 0, 1, 2, 3, 4, 5] and you want to delete 1, 3, 4.
Delete element 1-0 = #1
That leaves [ 0, 2, 3, 4, 5]
Delete element 3-1 = #2
That leaves [ 0, 2, 4, 5 ]
Delete element 4-2 = #2
That leaves [ 0, 2, 5]
You have correctly removed 1, 3, and 4.
The method is correct.
The point is that to do this takes LONGER than the reversing method.