When you’re trying to make things in your program work faster, it’s important to remember a simple rule. On any given computer…

You cannot make the computer go faster. You can make it do less work.

Of course, to take advantage of that rule, you must be able to judge a given method of doing something, and compare that to a different way of getting the same result. In text-based languages, you at least have a hint: the ten-line solution is likely faster than the fifty-line solution. It’s not guaranteed, but if you have the source code to both methods, you can make a reasonable guess.

In LabVIEW, though, everything is a black box. The Fast-Fourier Transform is a single icon on your diagram, so is the function to add two numbers. You can’t judge a function’s speed by it’s icon (there’s an aphorism there somewhere).

Suppose your task is to convert an array of complex numbers to magnitudes. The mathematical rules are not that complicated: M= sqrt(R²+I²). That’s two array multiplies, one array addition and one array square root.

But wait: there’s a function in the complex arithmetic palette to do this for you: Complex to Polar (C to P). It takes an array of complex numbers, and gives an array of magnitudes and an array of angles. That’s what you want, right?

The true speed freaks among you will immediately recognize a problem: This function does MORE than you need: you also get the angles associated with the complex numbers. And if you remember your basic trigonometry, calculating the angle is the more complicated of the two rectangular-to-polar operations. There’s the arctangent to compute, and the edge cases to deal with.

So if you’re interested in the speed of getting this done, the question becomes which one is faster? It’s certainly easier to plunk the C-to-P function down and throw away the angle numbers it produces. But suppose the speed of programming it is less important that the speed of executing it. There’s this nagging suspicion that the ANGLE calculations might be a fly in the ointment. So how do you test this?

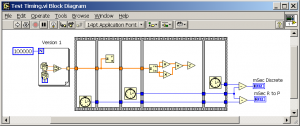
It sounds simple: Just remember the mSec timer before doing the operation, do the operation, remember the mSec timer after the operation, and figure the difference of the two timers. Version 1 shows this approach:

Looks simple enough. When you run a test like this, you generally should disregard the timing of the first run, because the compiler has just run and it is still shutting down as your program starts up. I always take three readings, to verify that this has settled down. And the answers I got are:

13, 14, and 12 for the Discrete method, and 0, 0, and 0 for the C to P method.

Well, isn’t THAT interesting?

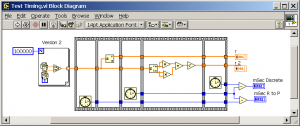
Obviously, that has to raise some suspicion. We’re not measuring what we think we are. Although the code looks right, it can’t do it that fast, it just can’t. Even raising N to 10 million shows the C-to-P operation taking zero time. To see what’s going on, we add indicators to the results. Since we don’t want to measure the display time, we put those indicators OUTSIDE the timing chain:

We run it four more times (ignoring the first) and get:

19, 18, and 19 for the discrete case, and 7, 7, and 7 for the C-to-P case.

What does that tell us? Well, if we give LabVIEW some credit for being smart, then we might say that it doesn’t compute results that it’s not going to use. If there’s no wire on the output, then it doesn’t perform the function at all! This leads to the question: Is it smart enough to do that on for each terminal separately, or does it go all-or-nothing? Simply adding another indicator answers that question – it takes longer to compute magnitude AND angle, than it does to compute magnitude only. No surprise, but that does reinforce our conclusion that LabVIEW is smart enough to help out. It’s only computing what we need to use.

Note that this applies only to built-in (yellow) functions. That’s because the compiler can tell whether we’re using the results or not. This might not apply to library functions, because they don’t have such a direct connection to the compiler.

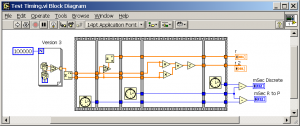
So, to answer our starting question: it is indeed faster to use the C-to-P function and disregard the angle outputs. But be careful, because the exact answer you get depends on the exact question you ask. The example above assumes you have the numbers in complex form already. Note that in version 3, the Complex-to-Real-and-Imaginary function has been pulled OUTSIDE the timing chain, meaning the discrete version stands a better chance of competing.

Here the timing results were:

10, 10, and 9 for the Discrete method, and 12, 12, and 12 for the C to P method.

That’s because the C-to-P method has to convert the real and imaginary parts to complex before using them.

Template

If you do a lot of that sort of work, you don’t want to construct the timing thing from scratch every time. I have a template VI that I use for such things, and it has extreme accuracy.

Over and above the example method shown, this VI has the following features:

• It’s a template, not a VI. That means whenever you open it, it forgets its file name and you have to save it somewhere else. This keeps it clean for the next time. If you want to save a particular version, go ahead, but when you open the template again, it’s empty and ready.
• It allows you to set the number of iterations, and provides an AVERAGE time per iteration. An operation that takes a microsecond can’t be timed with a millisecond timer, so you have to use 10000 operations or so. But an operation that takes a second can be measured with only one iteration.
• It compensates for the loop-execution overhead. If your loop runs 10 million times, the loop itself takes time. That time is removed for you.
• Since the example above proved that you MUST store the results somewhere to time something accurately, you might want to subtract out the storage time. In that case you can STORE (X[]) in the first loop and STORE (f(X[ ]) in the second. The cost of the actual storage is accounted for you.

Click to Download the Template (24 kB, unzipped, in LV 7.0 format).

Enjoy.